A is a scalene triangle and each side has a different measure Since it's a right triangle, the sides touching the right angle are called the legs of the triangle, it has a long leg and a short leg, and the hypotenuse is the side across fromNotice that when you are working with a 30º60º90º triangle you are working with Look at all of the THREEs at work! The 30 60 90 triangle is special because it forms an equilateral triangle when a mirror image of itself is drawn, meaning all sides are equal!

30 60 90 Special Right Triangle Calculator Inch Calculator
Special triangles 30 60 90 worksheet
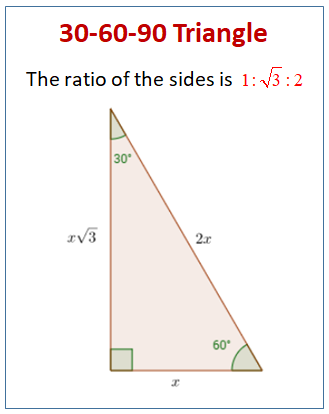
Special triangles 30 60 90 worksheet-A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 Any triangle of the form can be solved without applying longstep methods such as the Pythagorean Theorem and trigonometric functionsA triangle with angle degree measures of 30, 60, and 90 is a special right triangle;




How To Use The Special Right Triangle 30 60 90 Studypug
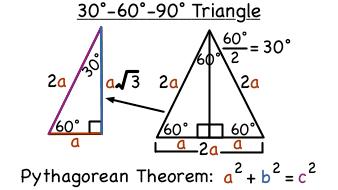
A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangleTriangles Theorem 2 In a triangle whose angles measure 30 0, 60 0, and 90 , the hypotenuse has a length 0 equal to twice the length of the shorter leg, and the length of the longer leg is the product of 3 And the length of the shorter leg The ratio of the sides of a triangle are x x 3 2 x Note The short leg is always
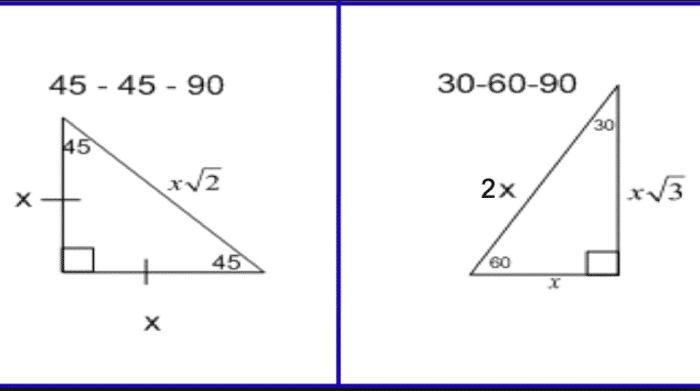
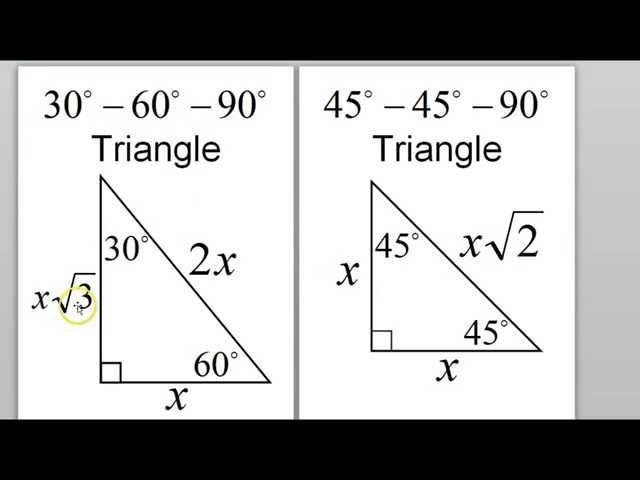
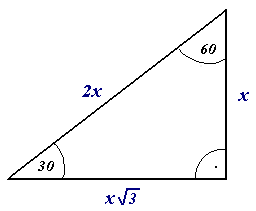
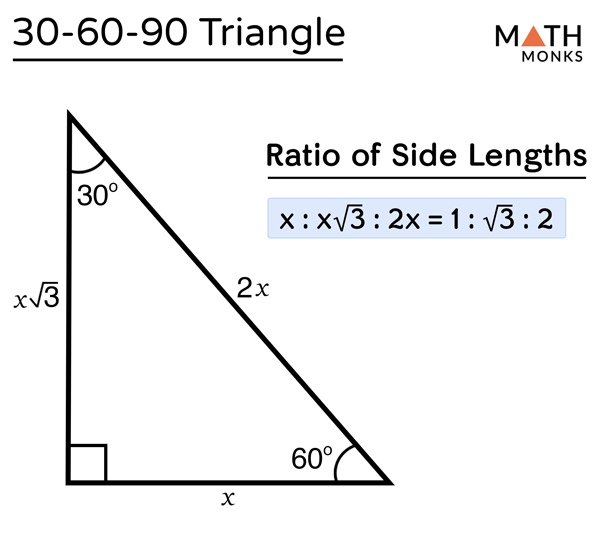
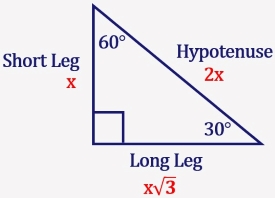
30 60 90 Triangle Ratio A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another36 Special Right Triangles () Name_____ Date_____ ©Y z2g0D1s7y ZKruAtZah BSZocf_tawhaerIed WLzLYCdn q AulMlS LrziXgYhEtTsF grVeCsVecrqvqedf1Find the missing side lengths Leave your answers as radicals in simplest form 1) a113 2 b 30° a = 11, b = 11 2 2) yx 23 60° x = 43, y = 6 3) 3x y 60°The triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 and the sides are in the ratio 1√3 2;
Special Right Triangles Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesIn plain language, the hypotenuse is twice as long as the shortest leg (opposite the 30 degree angle), and the longest leg (opposite the 60 degree angle) is √3 times longer than the shortest legTriangles The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and



Special Right Triangles Proof




5 30 60 90 Triangles Geometry15a
Special right triangles use the 30 60 90 and 45 45 Example 1 special right triangles Then find the value of x Such triangles are formed by the diagonals of a square Some of the worksheets displayed are find the missing side leave your answers as, 5 8 special right triangles work answers pdf, special right triangles work name, special right The other most well known special right triangle is the triangle In a triangle, the two nonright angles are 30 and 60 degrees Credit Public Domain A triangle has sides that lie in a ratio 1√32 Knowing these ratios makes it easy to compute the values of the trig functions for angles of 30 degrees (π/6) and A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another




30 60 90 Right Triangles Read Geometry Ck 12 Foundation




Special Angles Larger Than 90º
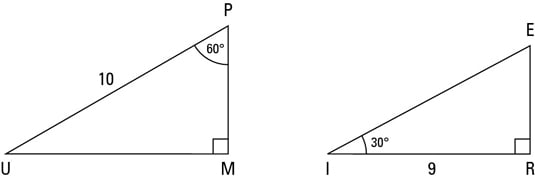
Multiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuseThe 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progression The proof of this fact is simple and follows on from the fact that if α, α δ, α 2δ are the angles in the progression then the sum of the angles 3α 3δ = 180° After dividing by 3, the angle α δ must be 60°Special Right Triangles Use the and triangle relationships to solve for the missing sides Use the answers to reveal the name of the team that Abraham M Saperstein established and sent on the road in 1927
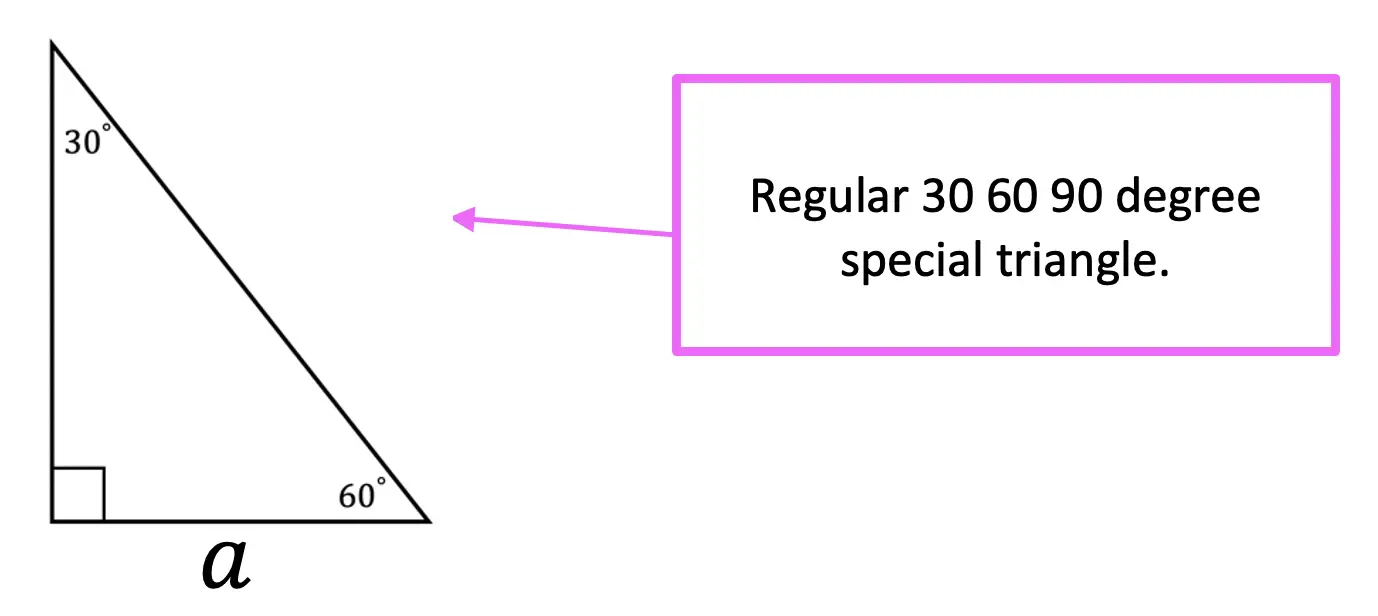



30 60 90 Special Triangles Geometry Mathsux 2




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
Likewise again 30 60 90 right Triangle 30 60 90 Let's say I know that the leg over here is 12 or three Well, now I know that the base or the other leg that's opposite the 30 degree side is 12 and that the iPod news is 24 all because of the special relationship that we get by cutting the collateral triangle in half, you get 2, 30 60 90 right triangles, and then what happens is the special Use the properties of special right triangles to find the length of the shadow created given each angle of sunlight angles are supp Trapezoid Kite 4 sides 2 ( sides 1 pair of opp ASSIGNMENT Isosceles Right Triangle Worksheet Grade Monday, 1/14 30°60°90° Triangles I can solve for the 2 missing sides of a 30°60°90° ASSIGNMENT 30°60°90° Worksheet90 ° Triangle Let's have a short introduction of these special right triangles as we will see them thoroughly in the next articles The 45 °;




30 60 90 Triangle Definition Theorem Formula Examples




How To Use The Special Right Triangle 30 60 90 Studypug
Special Right Triangles in This need to be a triangle due to the two given angles The partnership tells us that the side lengths are a, 2a, and a √ 3 We can see that a = five from the two given sides, and we are missing the 2a side So, the 3rd side size is 2 5 =10 Problem 3 A triangle with angles has side sizes of as well as 48This is right triangle whose angles are 30°60°90° The lengths of the sides of a 30°60°90° triangle are in the ratio of 1 √3 2 You can also recognize a 30°60°90° triangle by the angles As long as you know that one of the angles in the rightangle triangle is either 30° or 60° then it must be a 30°60°90° special right triangle
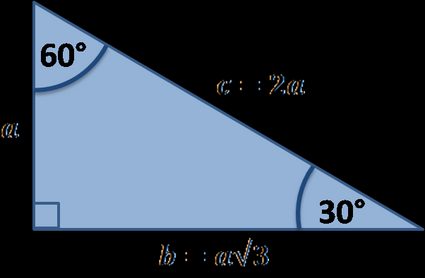



30 60 90 Triangle Calculator Formula Rules




Special Right Triangles Gmatsyllabus Com
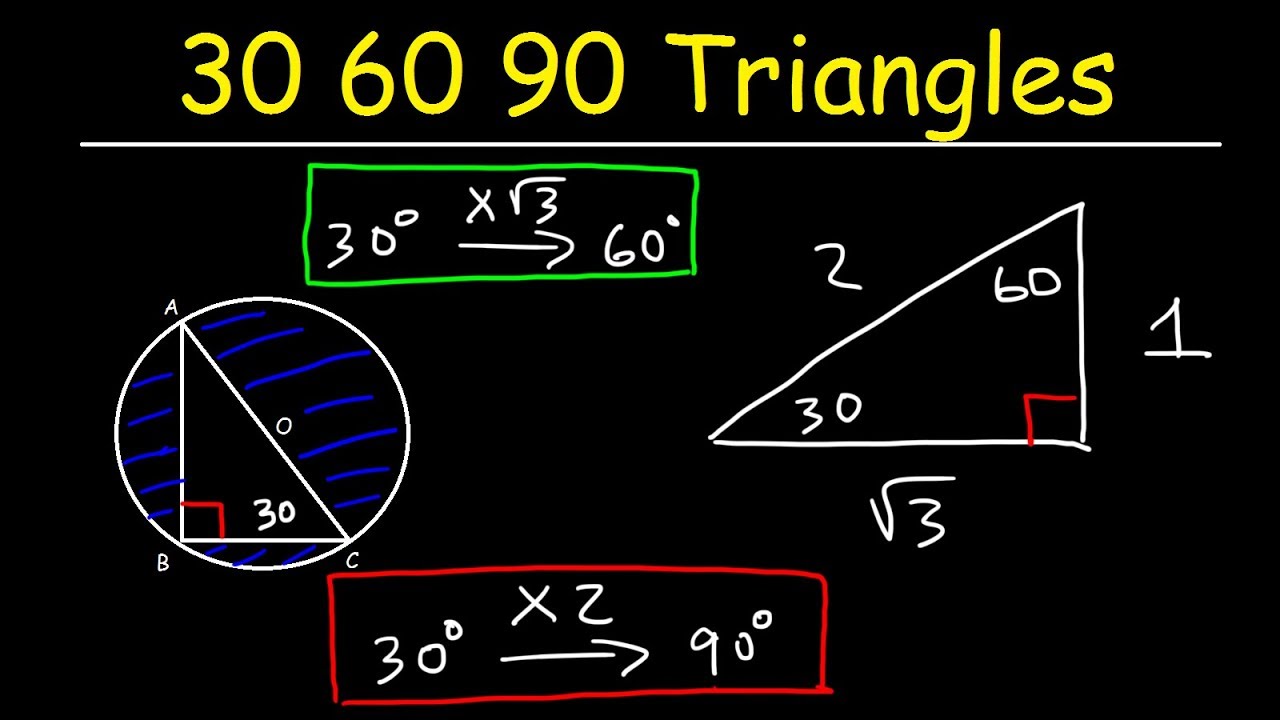
Theorem Application of Pythagoras #short #shortvideo #shortsfeedJustification The triangle was originally an equilateral triangle with three 60° angles The equilateral triangle was split down the middle, so α = 30° The other two angles on the side were not changed, so β = 60° Remember that the angles in a triangle must sum up to 180 ° Notice that 30° 60° 90° = 180° 1 cm cm 3 30° 60° 2 cmA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1√3 2
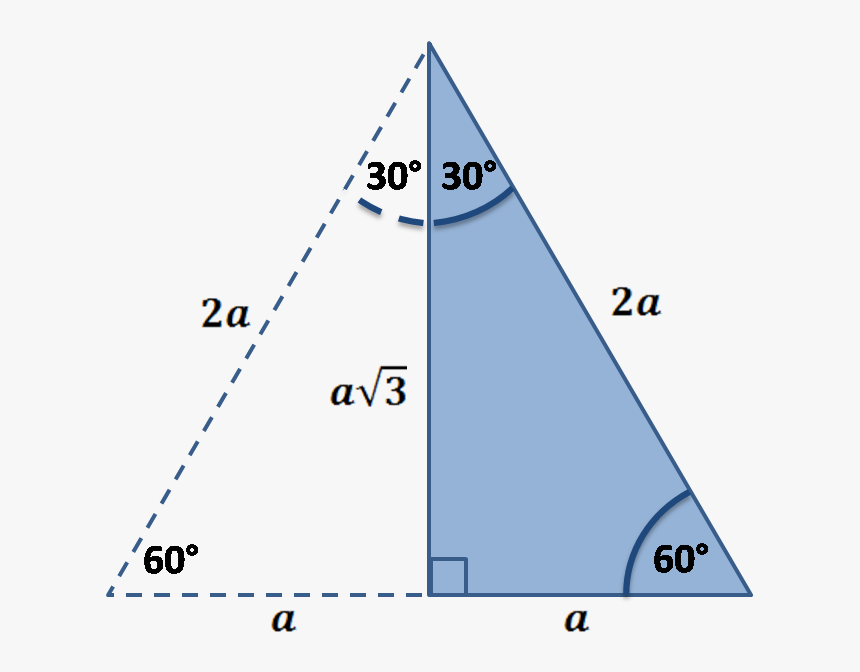



Using The Properties Of The Equilateral Triangle 30 60 90 Triangle Solver Hd Png Download Kindpng




Special Right Triangle Wikipedia
$1 per month helps!!A 30°60°90° triangle is a right triangle that contains the acute angles 30° and 60° The sides of these triangles have lengths with special proportions We can obtain these proportions using the Pythagorean theorem For this, we can consider that the 30°60°90° triangle is half of an equilateral triangle as shown in the following diagram We can assume that one of the short sides of the 30°60°90° triangle Triangle Practice Name_____ ID 1 Date_____ Period____ ©v j2o0c1x5w UKVuVt_at iSGoMfttwPaHrGex rLpLeCkQ l ^AullN Zr\iSgqhotksV vrOeXsWesrWvKe`d\1Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30° 2) 72 ba 30° 3) x y 5 60° 4) x 133y 60° 5) 23 u v 60° 6) m n63




How To Work With 30 60 90 Degree Triangles Education Is Around
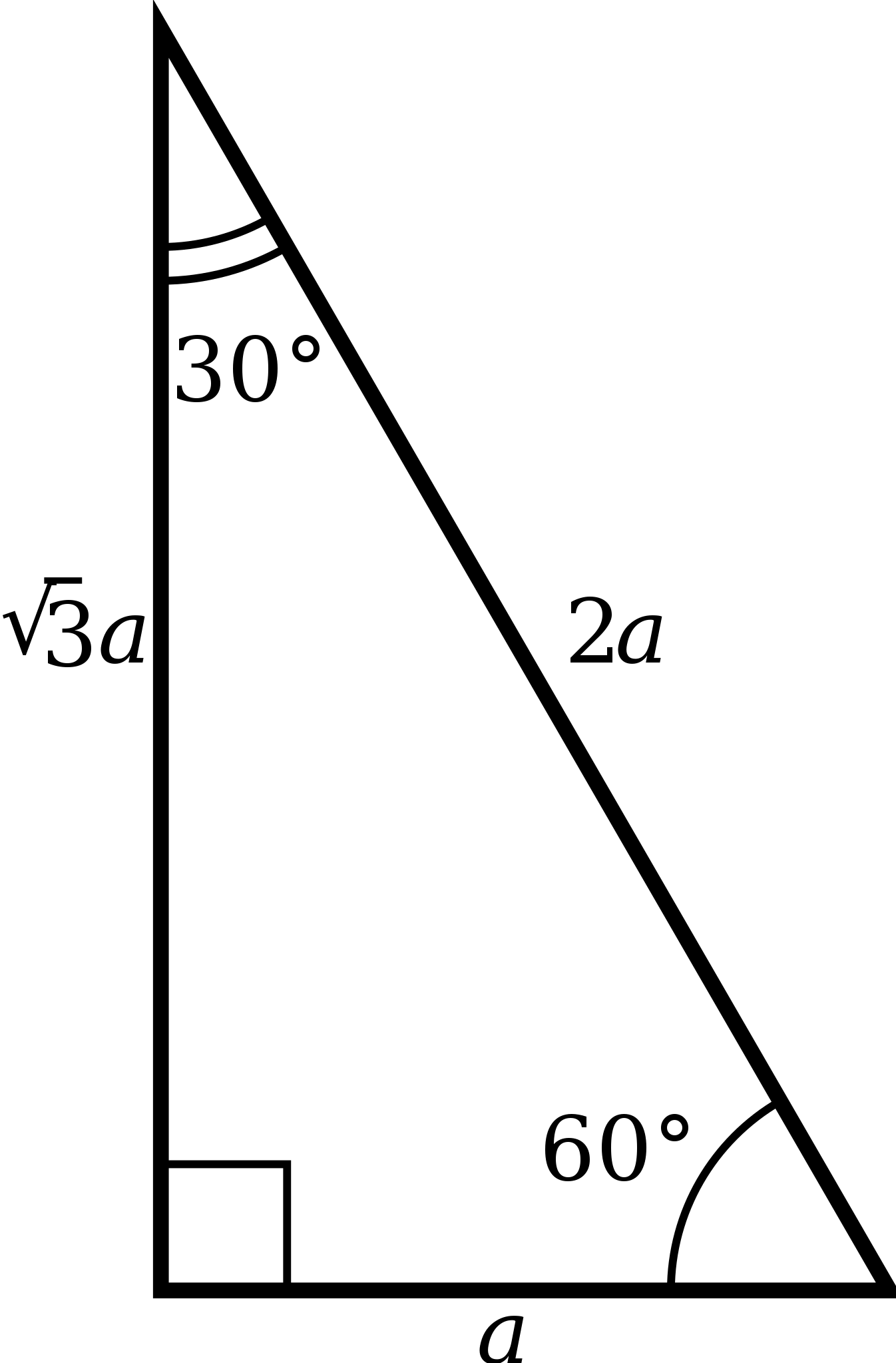



File 30 60 90 Triangle Svg Wikipedia
90 ° Triangle In particular, the right triangle angles are 45 °, 45 °, and also 90 °Thanks to all of you who support me on Patreon You da real mvps!Check out this tutorial to learn about triangles!



1



30 60 90 Triangle Formulas Rules And Sides Science Trends
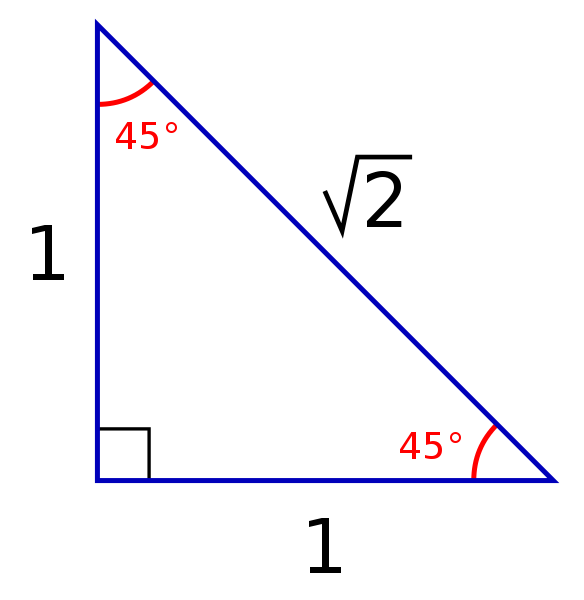
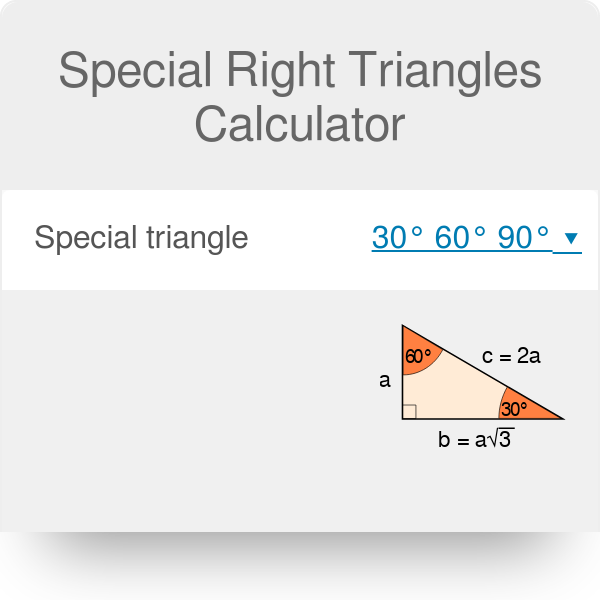
As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x The side opposite the 60° angle x * √3 The side opposite the 90A triangle is a right triangle where the three interior angles measure 30° 30 °, 60° 60 °, and 90° 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sides90 ° Triangle 30 °;



Special Right Triangles Complete Reference Guide The Education



What Is A 30 60 90 Degree Triangle Virtual Nerd
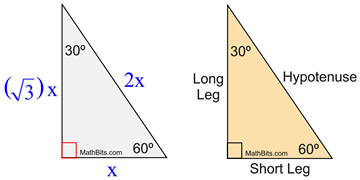
The common anglebased special right triangles are Triangle Triangle The triangle name describes the three internal angles These triangles also have side length relationships that can be easily memorized The image below shows all angle and side length relationships for the and triangles30, 60, 90, When you work with 30º60º90º and 45º45º90º triangles, you will need to keep straight which radical goes with which triangle 30 6090 triangles 1 Special Right Triangles 30 – 60 – 90 Triangles 2 Special Right Triangles Directions As you view this presentation, take notes and work out the practice problems When you get to the practice problem screens, complete the step in your notebook before continuing to the next slide 3



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video
Learn shortcut ratios for the side lengths of two common right triangles 45°45°90° and 30°60°90° triangles The ratios come straight from the Pythagorean theorem Both Special right triangles include 45 °; Special right triangles will always include a 90degree angle The special right triangles also have standard angle measures the triangle and the triangle You can use the unique properties of special right triangles to find the lengths of all three sides given one side length




30 60 90 Triangle Theorem Ratio Formula Video



Special Right Triangles 30 60 90 Math Geometry Triangles Right Triangles Showme
Triangles are special because they are exceptionally strong Out of all the twodimensional shapes we can make out of straight struts of metal, only a triangle is rigid Also, what are special triangles in trigonometry?A triangle is a special right triangle that always has angles of measure 30°, 60°, and 90° All the sides of a triangle can be calculated if any one side is givenThis allows us to find the ratio between each side of the triangle by using the Pythagorean theorem Check it out below!
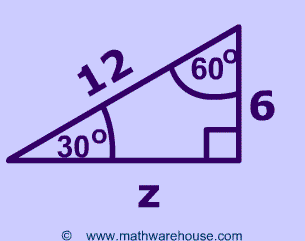



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



Right Triangle Degrees 30 60 90 Clipart Etc
A triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º angle, a 60º angle, and a 90º angle Since these angles stay the same, the ratio between the length of the sides also remains the sameHere is a triangle pictured below Figure % A triangle The other common right triangle results from the pair of triangles created when a diagonal divides a square into two triangles Each of these triangles is congruent, and has angles of measures 45, 45, and 90This video demonstrates how to solve degree triangle real life problem In this demonstration, we will examine how to solve for the height of the b




A Quick Guide To The 30 60 90 Degree Triangle Dummies
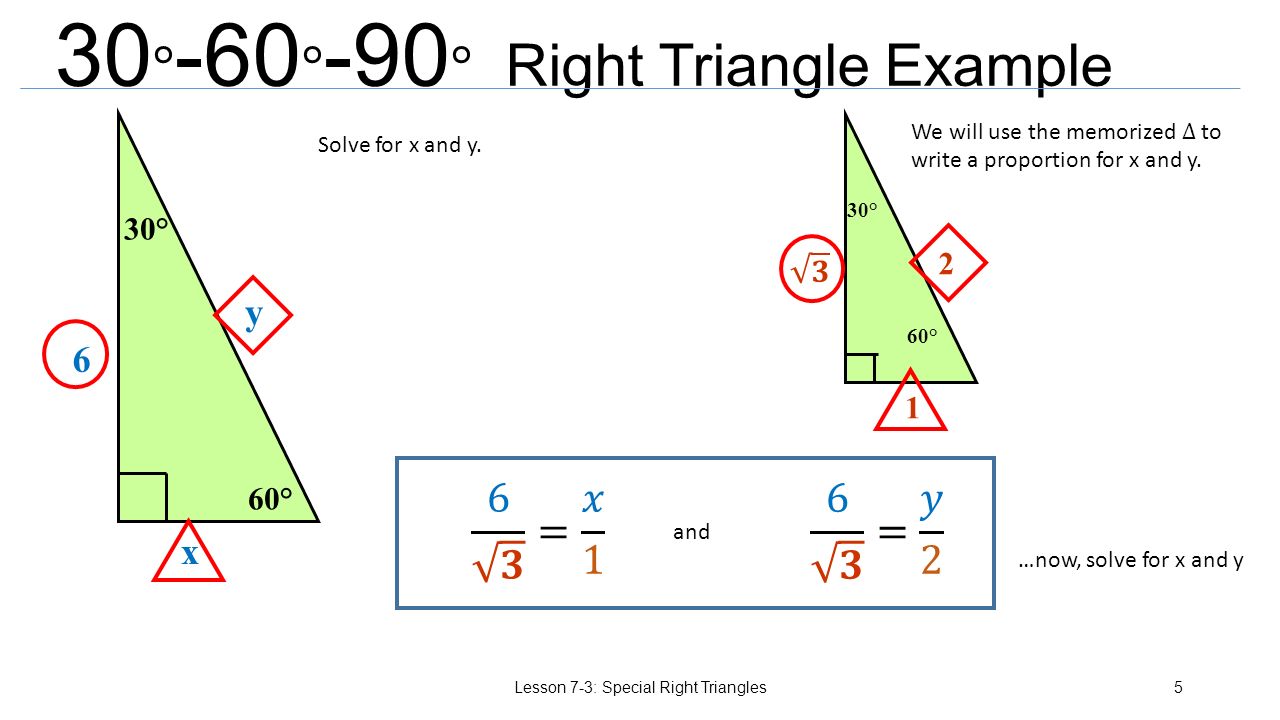



Special Right Triangles Lesson 7 3 Special Right Triangles1 Ppt Download
The special nature of these triangles is their ability to yield exact answers instead of decimal approximations when dealing with trigonometric functions C sekhar r anumapuram created date 1 m72 2 n 45 2 m n23 45 45 90 triangles 30 60 90 triangles Leave your answers as radicals in simplest form 1 a 2 2 b 45 2 4 x y 45 3 x y 3 2 2 45 4 x yCorresponding to opposite angle measures, the ratio of the side lengths of every triangle is 1√32; 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!




30 60 90 Triangles Special Right Triangle Trigonometry Youtube
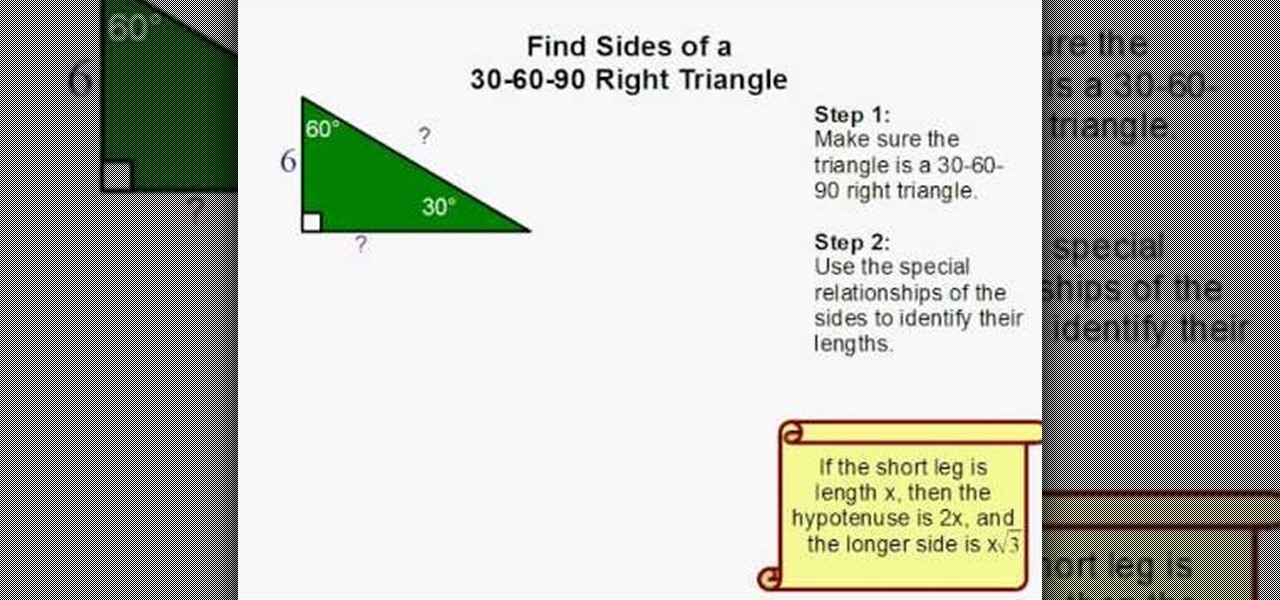



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto



Special Right Triangles 30 60 90 Worksheet Jobs Ecityworks




Test Prep Thursday Special Right Triangles Mathnasium



30 60 90 Special Right Triangles For Act Sat Math Geometry Trigonometry Youtube




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




A Quick Guide To The 30 60 90 Degree Triangle Dummies



What Is The Area Of A 30 60 And 90 Triangle If The Hypotenuse Is 12 In Quora



Special Right Triangles Calculator Formula Rules




The 30 60 90 Triangle Topics In Trigonometry




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies



Identifying The 30 60 90 Degree Triangle Dummies
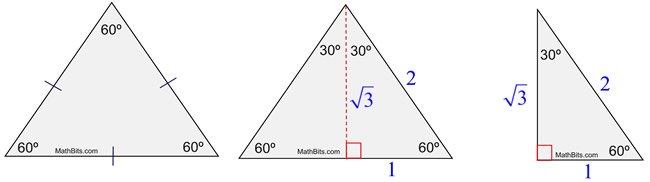



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




30 60 90 Triangle Theorem Ratio Formula Video
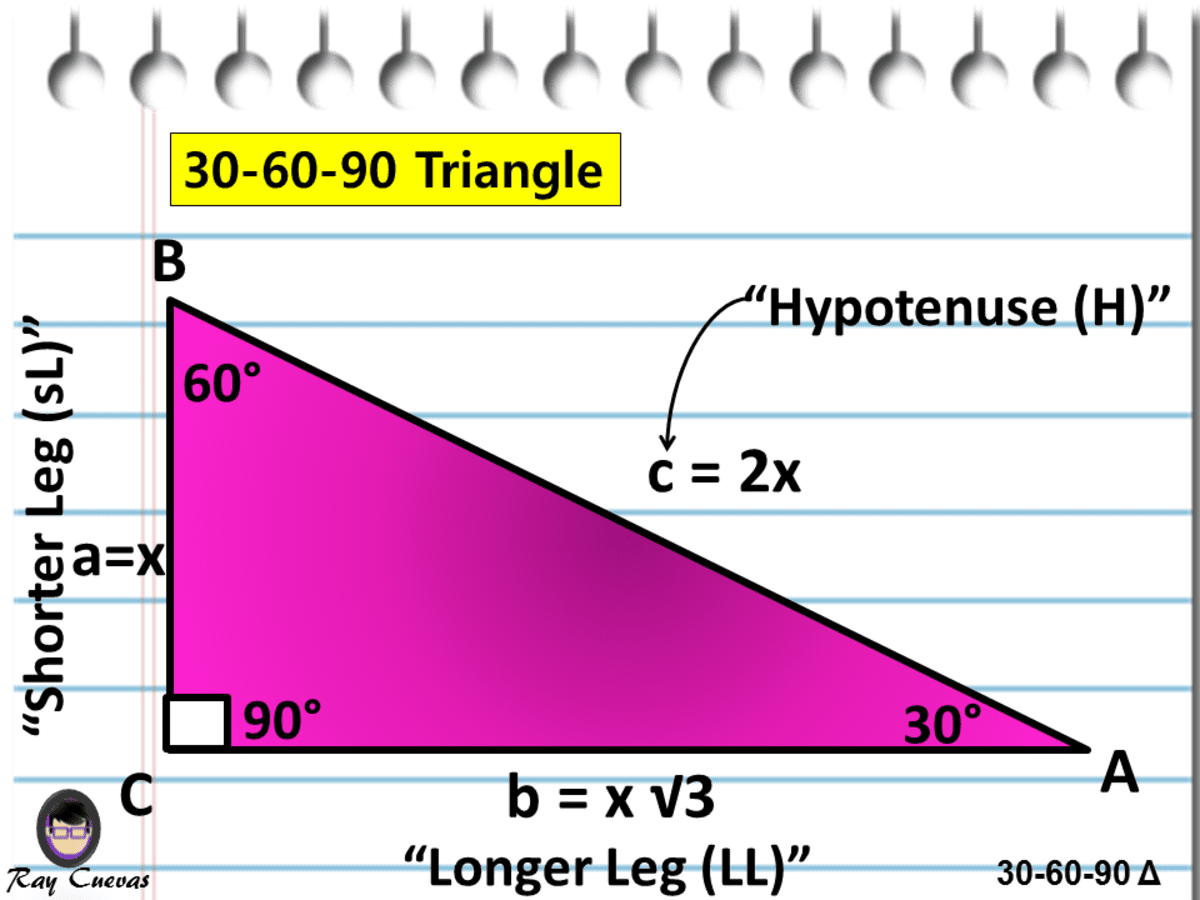



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



3
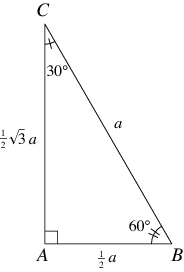



30 60 90 Triangle From Wolfram Mathworld



45 45 90 And 30 60 90 Triangles Zona Land Education




30 60 90 Special Right Triangle Calculator Inch Calculator




Sat Triangles 30 60 90 Youtube




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Special Right Triangle Calculator General Knowledge Book Right Triangle Electrical Engineering Books
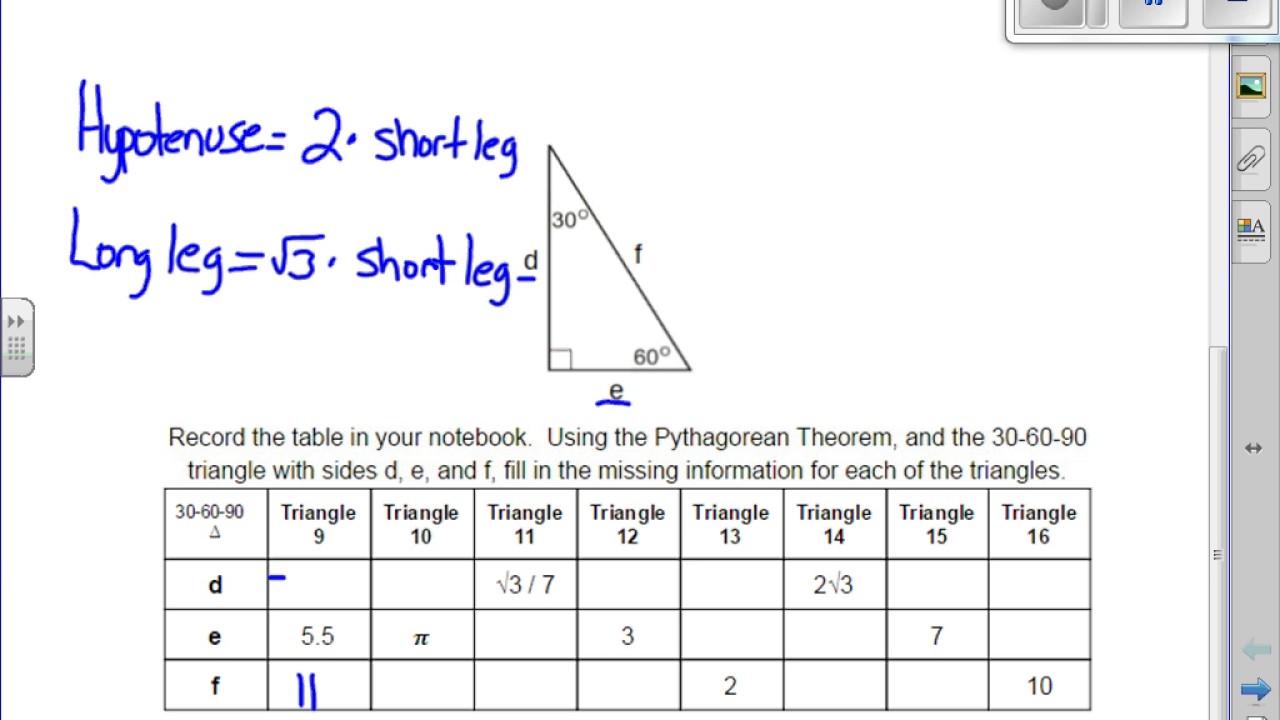



Special Right Triangle 30 60 90 Tutorial Youtube



1




30 60 90 Triangles
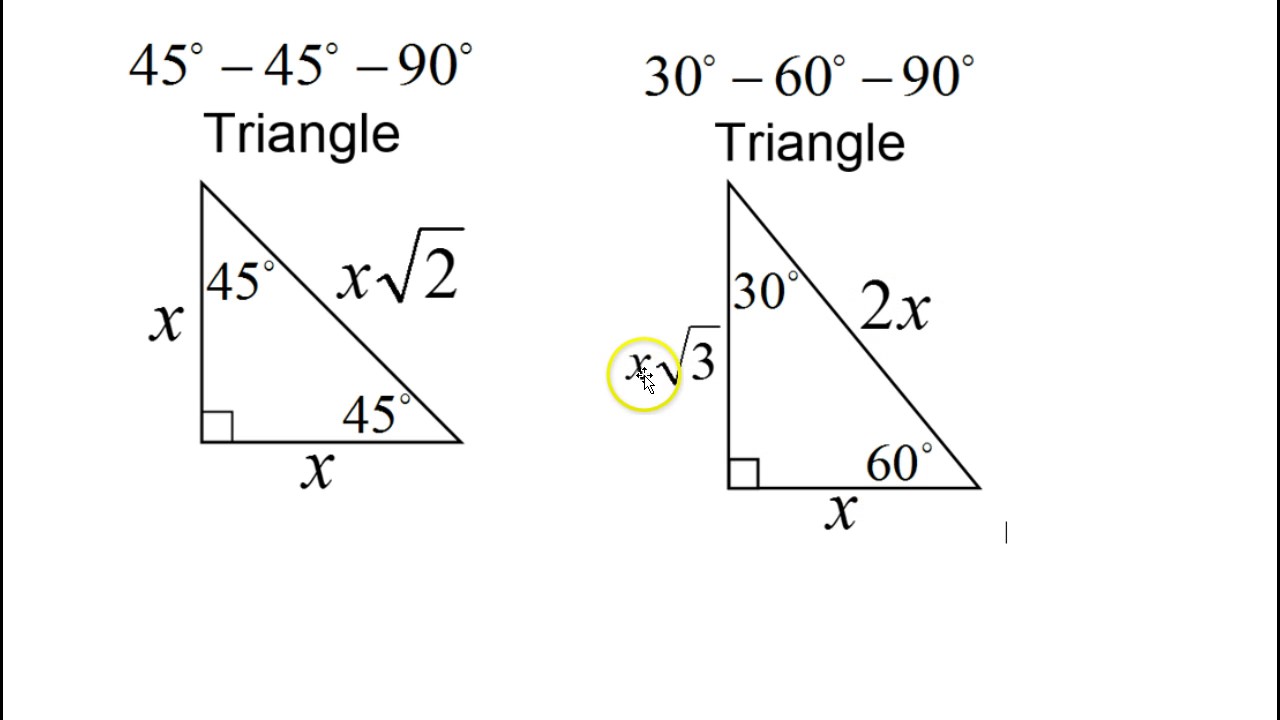



Day 16 Test C 9 To 12 Special Right Triangles 30 60 90 45 45 90 Youtube




30 60 90 Triangle Calculator Formula Rules
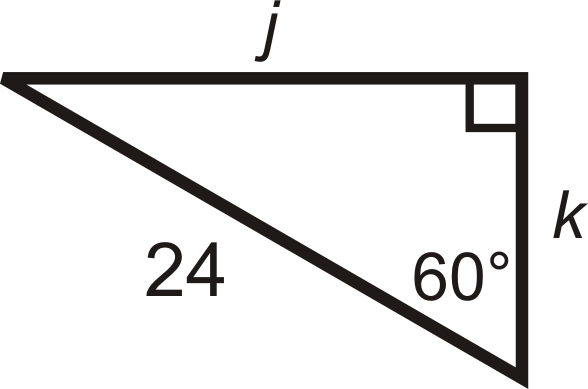



30 60 90 Right Triangles Read Geometry Ck 12 Foundation
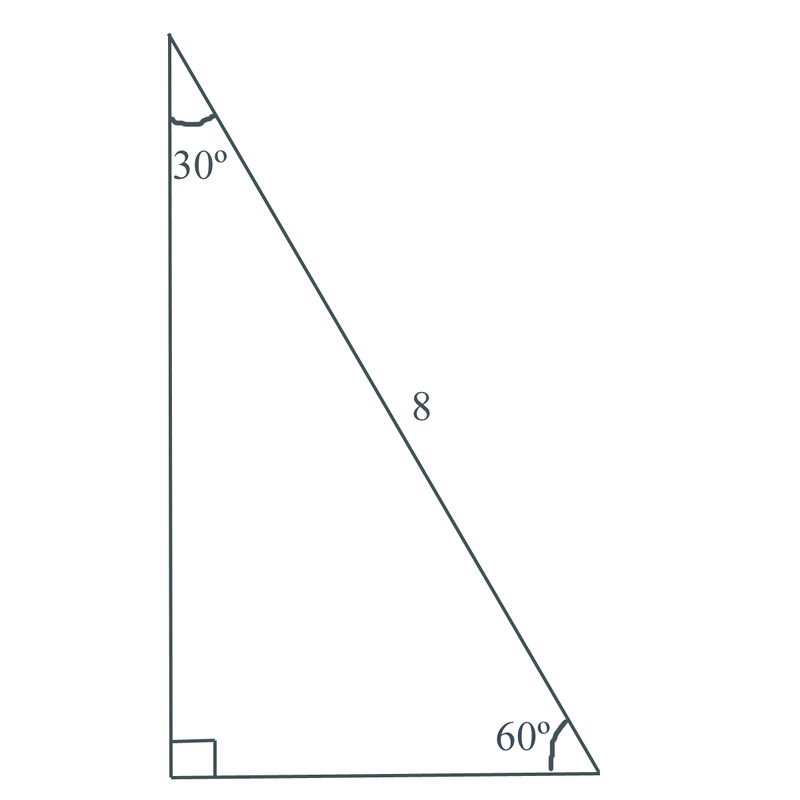



Relationships Of Sides In 30 60 90 Right Triangles Read Geometry Ck 12 Foundation



Is A 3 4 5 Triangle Also A 30 60 90 Triangle Quora
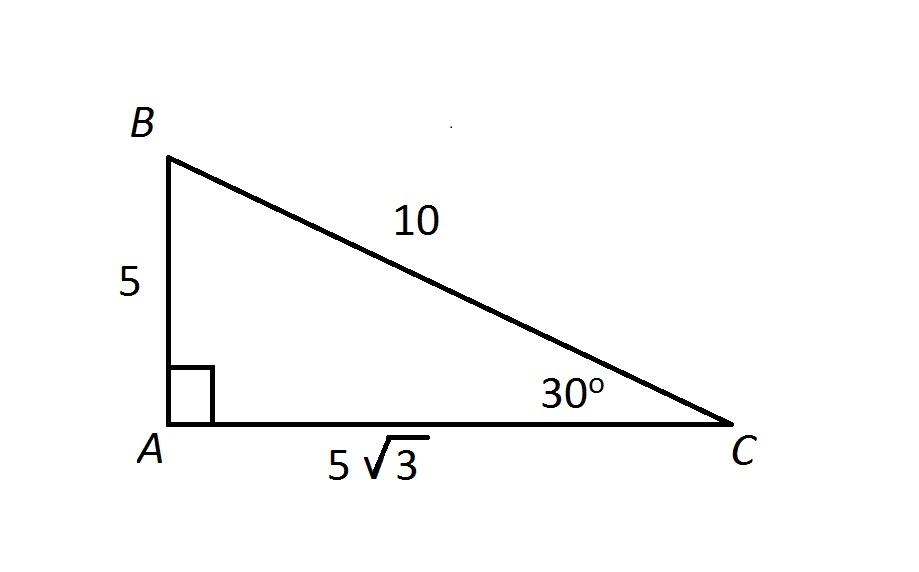



Special Triangles Hiset Math



Trig




File 30 60 90 Triangle 2 Svg Wikimedia Commons




Special Right Triangles 30 60 90 And The 45 45 90 Graphic Organizer Worksheet Special Right Triangle Right Triangle Word Problem Worksheets




30 60 90 Right Triangles Read Geometry Ck 12 Foundation



Special Right Triangles Proof




The Complete Guide To The 30 60 90 Triangle




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



File Triangle 30 60 90 Rotated Png Wikipedia



Mrwadeturner 30 60 90 Triangle 6th




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




Relationships Of Sides In 30 60 90 Right Triangles Read Geometry Ck 12 Foundation




Special Right Triangles Video Lessons Examples And Solutions




Special Right Triangles Fully Explained W 19 Examples



30 60 90 Triangle Definition Formulas Examples




30 60 90 Right Triangles Free Math Help



Special Right Triangle 30 60 90 Mathondemand Com



The Easy Guide To The 30 60 90 Triangle




Learn About The 30 60 90 Triangle Caddell Prep Online




30 60 90 Triangles Spock S Guide To Math 4




30 60 90 Triangle Calculator Formula Rules



Triangle 30 60 90 Clipart Etc
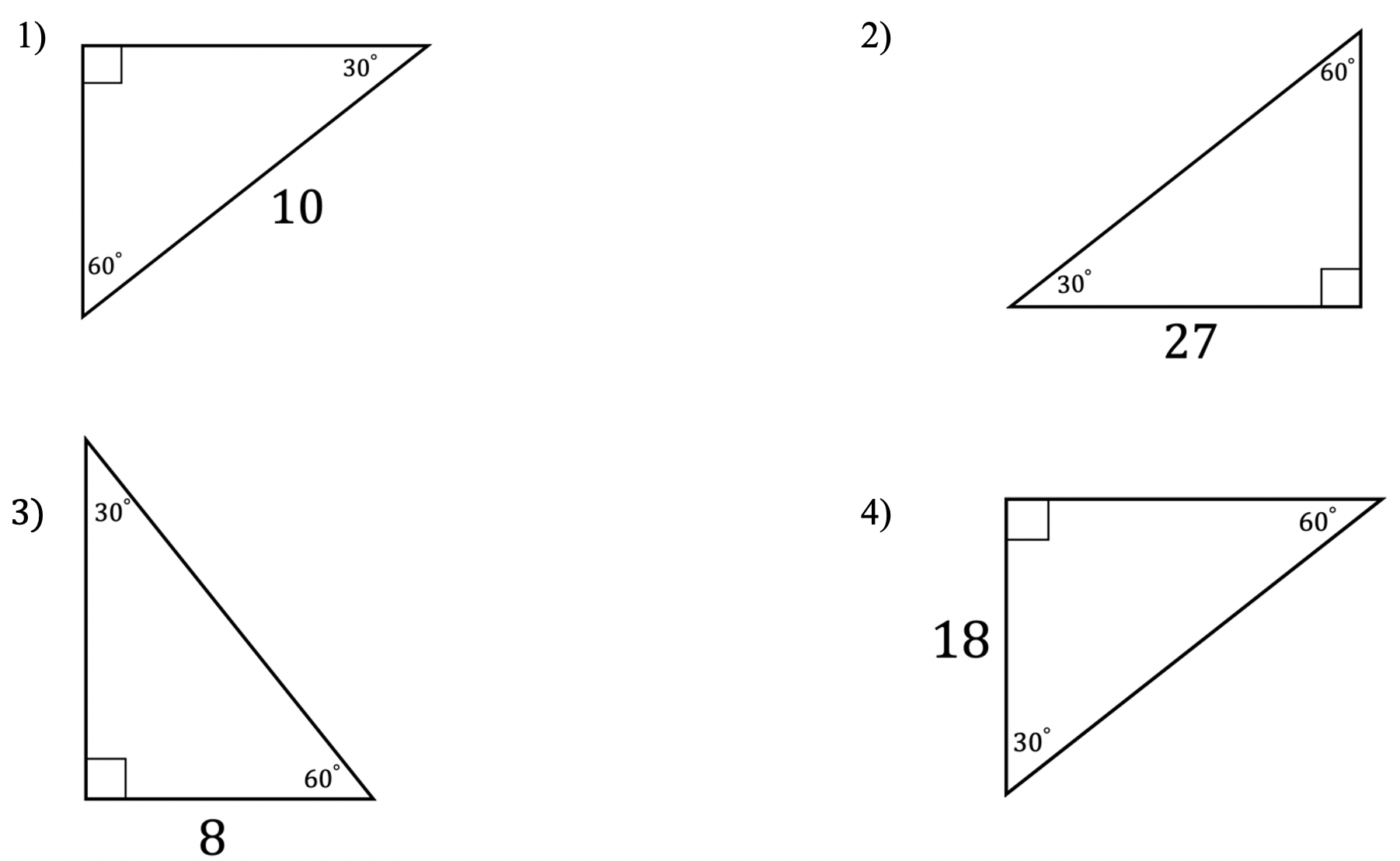



30 60 90 Special Triangles Geometry Mathsux 2
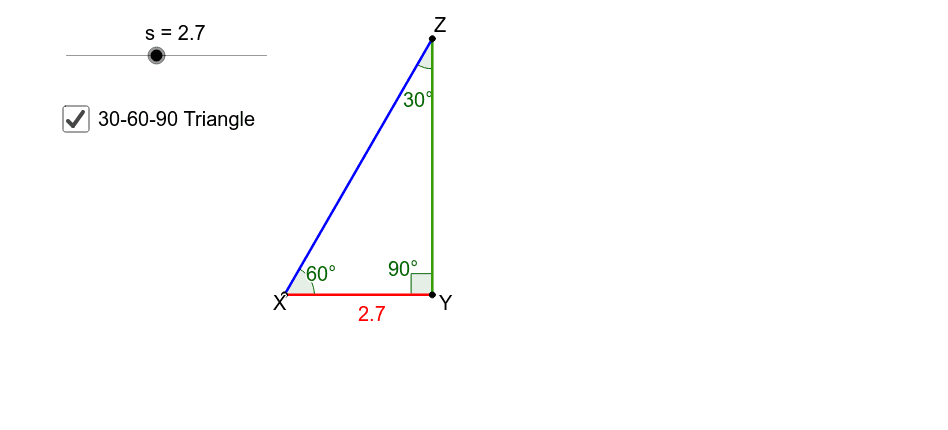



Special Right Triangles 30 60 90 Geogebra




8 2 Special Right Triangles Ppt Video Online Download




30 60 90 Triangle 30 60 90 Triangle Png Transparent Png 403x401 Free Download On Nicepng



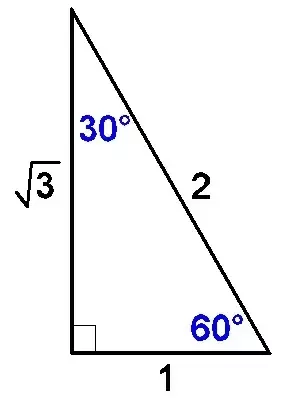
Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



Lesson 1 Special Right Triangles 30 60 90 Frys Nc Math 2 Honors S2




30 60 90 Triangle




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



30 60 90 Right Triangle How Do I Solve If The Long Leg Is 10 Socratic




Special Angles In Quadrant Ii 30 60 90 Triangle Quadrant 2 Transparent Png 360x368 Free Download On Nicepng




30 60 90 And 45 45 90 Triangles Youtube




Right Triangles Special Right Tris Notes Practice Task Cards Riddle Bundle Special Right Triangle Right Triangle Math Notes




Special Right Triangles Review Article Khan Academy




30 60 90 Right Triangles Solutions Examples Videos




The Complete Guide To The 30 60 90 Triangle



Solve A 30 60 90 Triangle With Gradea



30 60 90 And 45 45 90 Triangle Calculator




30 60 90 Triangle



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions
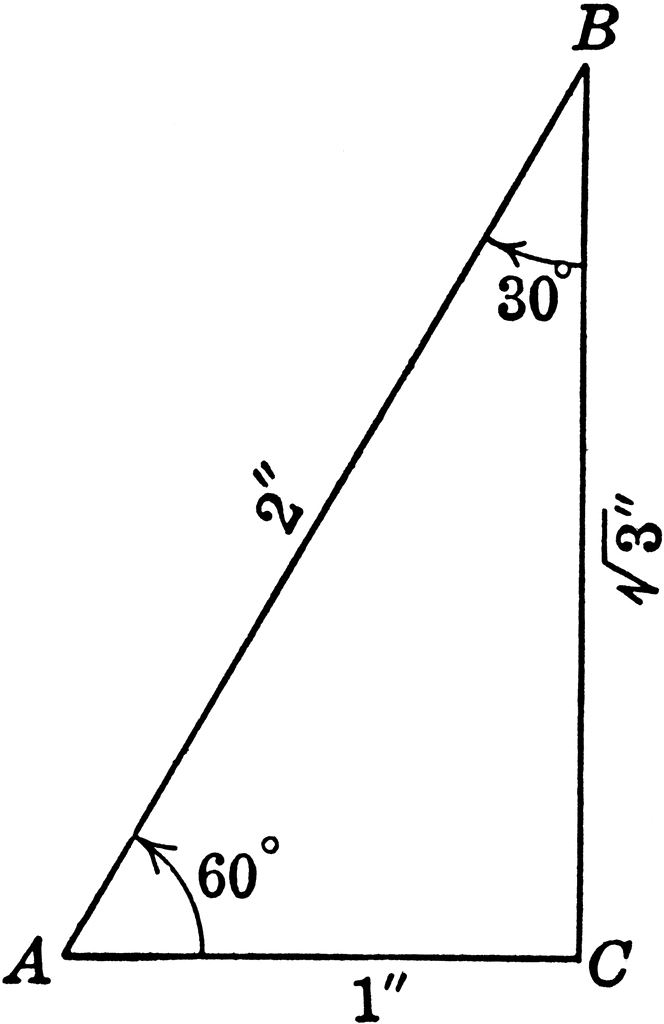



Special Right Triangle With Angles 30 60 90 Degrees Clipart Etc



Geometry Lesson 7 2 Special Right Triangles Lessons Blendspace




30 60 90 Triangle Explanation Examples



A 30 60 90 Triangle Math Central



0 件のコメント:
コメントを投稿